速看!多重共线性严重影响了你的数据科学项目!
原创:MarTechApe
多重共线性(Multicollinearity)是什么?
顾名思义,多重共线性是指两个(或多个)要素相互关联,即“共线性”。这通常发生在真实的数据集中,因为一个变量(例如家庭收入)可能与另一个变量(例如学校成绩)相关联,如此一来会对模型结果产生影响。你可能没有意识到许多算法和分析方法都依赖于没有多重共线性的假设。
当你要检查模型或分析的结果时,你可能有一个长长的checklist,比如R sqr,Error Rate,P Value等等,可是多重共线性可能根本不在要检查的这个清单上。但是,这确实几乎总是出现在现实生活的数据中,因此我们要知道如何解决它。
让我们以下面这个数据库为例,该数据库试图用一些因素来预测学生的入学机会,比如托福、GRE成绩,GPA和你学校的排名情况等等。
我们希望实现一个静态的状态,例如,“科研能使你被录取的机会增加x%”,或 “托福每增加一份,就可以使入学的机会增加y%”。我们首先想到的方法是训练线性回归模型并解释系数。
多元回归模型的平均绝对误差约为4.5%,这是相当准确的。系数的分析很有趣,GRE分数的系数是0.002,而GPA的系数是0.1135,我们可以这样说:“ 你的GRE每增加一分,你被录取的机会增加了0.2%,而GPA的每增加一分,你被录取的机会增加了11.4%。”
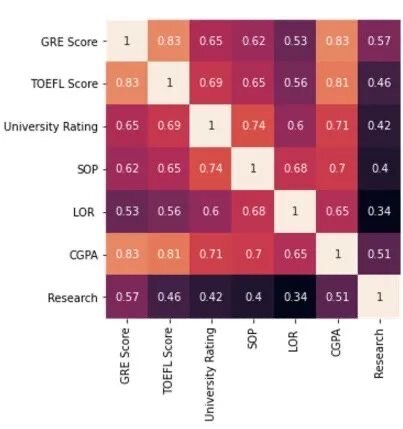
让我们看一下相关系数矩阵,来确定哪些变量是相互关联的。
总的来说,该数据充满了高度相关的特征,但是GPA通常与其他特征变量高度相关。
由于TOEFL分数与GRE分数高度相关,因此让我们将托福成绩这个特征变量从模型中剔除,然后重新训练线性回归模型。令人惊讶的是,平均绝对误差降低到4.3%。系数的变化也很有趣: 大学排名的重要性降低了近一半(从0.0097下降到0.0052),研究的重要性提高了一倍(从0.0132上升到0.0259)。如图:
从这个例子中我们可以了解到:
就像任何其他变量一样,TOEFL分数可以被认为具有两个组成部分:可以用来解释因变量的有用信息和“噪音”。
它的有用信息部分已经用其他变量表示出来了,比如GPA很高说明他的学习能力很强,GRE分数很高说明他的英语水平非常出色等等。因此它没有提供任何新的有用信息。
托福分数这个变量会带来很多“噪音”,为了获得最小的信息增益而保持该变量,不值得将它引入模型。
换句话说,托福成绩与许多其它变量是高度相关的(具有共线性)。从根本来说,模型的性能受到了损害,但更重要的是,它会对每个变量的系数造成影响,我们对模型结果的解读也会发生变化。
回归模型系数的含义值得我们探索。例如,如果GRE分数的系数为0.2%,意味着在所有其他变量的不变的情况下,GRE分数每增加1分,入学率就会增加0.2%。但是,如果我们包括TOEFL分数(以及其他高度相关的特征变量),我们就不能假定这些变量将保持不变。
因此,由于存在大量的信息重叠,所以这些系数非常混乱,而且完全无法解释。当出现这种情况时,建模能力也会受到限制。由于存在太多的重叠,因此所有用来解释因变量的特征变量功效都会被放大。如果一个部分出现错误,很可能会通过重叠,将错误延伸到其他部分。
通常,死记硬背算法和技术在多重共线性中是否能很好地工作是不切实际的,但是事实是,任何对特征变量“一视同仁”,不区别对待的假设或不考虑特征变量中,可以用来解释因变量的“有用信息”都会非常容易受到多重共线性的影响。
这是什么意思呢?
以决策树(decision tree)为例,决策树不易受到多重共线性的影响,因为它只提取特征变量中的有用信息来解释因变量,它的算法不会将变量与变量之间的相关关系考虑在内。如果A变量和B变量相互关联,则决策树将只选择其中一个而舍弃另一个(或将其重要性放置得很低)。在这种情况下,每个特征变量可以用来解释因变量的”有用信息“作为评判特征变量重要性的关键因素。
另一方面,K-最近邻算法受多重共线性影响,因为它假设每个点都可以在多维空间中表示为某个坐标(例如,在具有四个维度的x训练集上的(3,2.5,6.7,9.8)。它不会衡量有用信息的多少,会将这些特征变量视为相同。因此,可以想象两个高度相关的特征之间的数据点将沿着一条线聚集在一起,从而干扰跨维距离。
主成分分析(PCA)是一种无监督的方法,但是我们仍然可以按照这些标准对其进行评估。PCA的目标是明确保留数据集中的数据差异和结构,从而将一个复杂的数据集进行降维和简化,这就是为什么它不仅通常不受多重共线性影响,而且还经常被用来减少数据集中的多重共线性。
现实生活中常用到的一些分析方法和算法依赖于矩阵数学和线性代数系统,本质上是高维空间的表现,这很容易被多重共线性破坏。
例如虚拟变量(其中分类变量以0和1表示)因为它们形成了完美的线性关系,也可能被多重共线性破环。假设我们有三个二进制列A,B和C,它们的每一行将被归属于某一类别。这些列的总和必须加1,因此建立了完美的线性关系A + B + C = 1。
我们如何识别多重共线性?
在回归模型上使用VIF(方差膨胀系数/方差扩大因子)得分来确定数据集中是否存在多重共线性。
如果模型的标准差过高,则也可能表明由于信息重叠,一个错误正在重复传播。
添加或删除新特征变量时,参数的过大变化表示信息有很多重复。
创建一个相关系数矩阵。值始终高于0.4的要素表示与其他变量具有很强的多重共线性。
多重共线性有多种解决方案:
首选方法是获取更多数据。更多数据可以使模型保留当前足够的信息量,同时为数据中存在的”噪音“提供更多维度的考量。
使用那些不太受多重共线性影响的算法。岭回归,主成分回归,决策树或偏最小二乘回归都是很好的回归选择。
使用PCA可以减少数据集的维数,并且仅保留对于维持数据结构非常重要的变量。如果数据集总体上存在非常多共线性,这将是有益的。
使用特征选择方法剔除高度相关的特征。
想在履历上增添高含金量的数据科学项目?探索包多重共线性在内的多种统计建模问题与模型处理方法?秋招拿到理想offer?MarTechApe的宝藏项目《营销组合建模企业级实战训练营》就是专门培养营销数据科学家的企业级别实战项目,拥有企业真实数据(改编)与行业标准流程,项目经历可成为简历上的履历!9月26日就要开课啦!
训练营的学员收获了:
真正意义上的“用数据和模型解决营销中最重要的问题”的经历。
熟练掌握SQL、R、Tableau等时下最流行的数据处理语言,并用这些技能解决实际问题。
大大提高Media/Advertising Industry的商业意识,熟悉不同媒介渠道的广告活动对不同商业指标的不同回报率(ROI)与有效性(Effectiveness),学会用“营销效果”的视角看待营销活动,理解各大公司市场营销部门、消费者洞察部门的痛点。
跳出学校作业的框架,上手真正商业情境中、实际工作中的实战案例。让校园与实际工作无缝衔接。将学到的Analytics思维方式泛化到其他应用场景,面对Case Study建立系统性解决思路。
提升项目演示Presentation技能,学会如何从原始数据中挖掘具有意义的故事。为客户解决实际问题,提高Business KPI。
完成项目后,辅导老师将帮助你利用这一个惊艳的项目背景打造最引人注目的简历;所有学员获得内推机会,优秀学员获得一对一面试辅导。